Downloads, Korrekturen und Ergänzungen zum Buch
„Werkzeuge der Signalverarbeitung“
für 18.188.13.212
 Stand:
09.01.2020
Stand:
09.01.2020
- Link zum kostenlosen, werbungsfinanzierten Druckservice (Tipp von Mike)
- Zweite deutsche Auflage als PDF (Stand: 06.12.2018)
- Russische Auflage als PDF (Stand: 03.04.2019)
- Chinesische Auflage als PDF (Stand: 12.02.2019)
- Erste russische Auflage nur 4 Seiten (Stand: 21.03.2013)
- S. 15: In der eigenen Signaldefinition kann ergänzt werden: „Ein Signal ist im allgemeinen Fall ein Raum-Zeit-Objekt. Es ist an einen physikalischen Träger gebunden. In der zeitlichen und / oder örtlichen Veränderung seiner Parameter können Informationen enthalten sein.“
- S. 19, Gleichung 2.5:
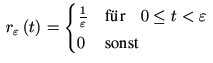

- S. 27: In Abbildung 2.12 sind die beiden ω-Achsen korrigiert.
- S. 33: Eine zeitgemäße, interaktive Version des Rechenschiebers in Abb. 2.17 (programmiert von Gérard Baecker).
- S. 34: In Gleichung 2.29 ist das j zu streichen.
- S. 36: Nach Gleichung 2.34 ist ein Satz zu ändern in: Die Filterordnung N ergibt sich durch die Wahl von ε und λ sowie durch die Wahl einer Grenzfrequenz ωg und einer Sperrfrequenz ωs.
- S. 42 Mitte: Entsprechend werden serielle und parallele AD-Umsetzer unterschieden. Die serielle Umsetzung, häufig über die Zwischengröße Zeit indirekt realisiert, erfordert viele Umsetzschritte (für 8 bit bis zu 255 Umsetzschritte), aber nur ein Normal. Sie ist langsam, aber wenig aufwändig. Die parallele Umsetzung, auch direkte Methode genannt, arbeitet mit nur einem Umsetzschritt, aber vielen Normalen. Bei 8 bit werden z. B. 255 Komparatoren benötigt.
- S. 66 oben:
Der Zusatz in der Klammer für das normierte z1 kann entfallen.

- S. 68:

- S. 69: Für eine diskrete Zufallsgröße ist der Median der kleinste aller Zufallswerte xi, für den F(x) ≥ 0,5 gilt.
- S. 82: In Gleichung 3.61 heißt der maximale Summationsindex Nh-1. Der Satz danach endet mit „... die Länge 2N-1“.
- S. 83: Gleichung 3.62 ist eine zweckmäßige Normierung für die AKF.
- S. 83: In Gleichung 3.63 heißt der Nenner N-|m|. Der Satz danach beginnt mit „... gleicher Länge N“.
- S. 83:
In Gleichung 3.64 ist der Nenner korrigiert:
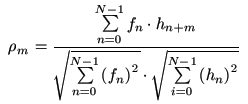
- S. 87: Abbildung 3.21 ist korrigiert.
- S. 90:

- S. 105:

- S. 109: Im Satz nach Gleichung 3.110 ist die folgende eulersche Beziehung gemeint: exp(-j·x) = cos(x)-j sin(x).
- S. 114: Gleichung 3.129 gilt für m≠k.
- S. 118: In den Gleichungen 3.143 bis 3.146 sollte die Variable n durch m ersetzt werden. Im Absatz nach Gleichung 3.146 ist die Festlegung der Abtastzeitpunkte tn=(n-1)T/N falsch, richtig ist tn=nT/N=nTA. In den Gleichungen 3.147 sollte ebenfallls die Variable n durch m ersetzt werden. Aber nur, wenn n ein Faktor vor ω ist. Im Index von tn bleibt n natürlich erhalten.
- S. 121: Die Ordnungszahl der Walshfunktionen entspricht der Anzahl der Nulldurchgänge im offenen Einheitsintervall Θ∈(0,1). In Gleichung 3.155 ist im Argument der sal-Funktion nicht i+i/2, sondern (i+1)/2 richtig. Die normierte Sequenz entspricht der halben Anzahl der Vorzeichenwechsel im linksoffenen Intervall Θ∈(0,1].
- S. 123: Im Satz nach Gleichung 3.160 ist mit dem Symbol ⊕ die bitweise Addition modulo 2 gemeint.
- S. 124: In Gleichung 3.162 ist vor dem ersten Funktionsnamen swal eine geschweifte Klammer { zu ergänzen. Die Klammer } folgt am Gleichungsende.
- S. 125: In Gleichung 3.166 ist vor dem Kroneckeroperator (nach Leopold Kronecker) ⊗ die Matrix Hn-2 durch die Matrix H1 zu ersetzen.
- S. 127: In Gleichung 3.169 ist dx durch dΘ zu ersetzen.
- S. 127:
In Abbildung 3.52
hat Henrik Zbierski diese Korrektur vorgeschlagen:

- S. 128 (Übung 13): Von einer kontinuierlichen Zufallsgröße x(t) ist die Wahrscheinlichkeitsdichtefunktion bekannt: p(x)=λ·exp(-λx) für x≥0 und p(x)=0 für x<0.
- S. 141: Für die folgenden Gleichungen wird eine Größe K benötigt, für die gilt 2K+1≤N. In Gleichung 4.12 beginnt dann die Summierung bei k=-K und endet bei K. In Gleichung 4.13 endet die Summierung bei K. In den Gleichungen 4.15 bis 4.17 läuft k jeweils nur bis ±K bzw. K.
- S. 142: Im Absatz vor der Überschrift muss es heißen: Der Abstand der Spektrallinien entspricht einer Grundkreisfrequenz 2π/N und für die Periodizität gilt ck=ck+N.
- S. 144: Der Summationsindex i in Gleichung 4.21 beginnt bei Null. Der Abstand der Spektrallinien im Sequenzspektrum entspricht dem Kehrwert der Periodendauer. Abbildung 4.5 zeigt nur den Beginn des Sequenzspektrums des Dreiecksignals fD(Θ) in Abbildung 4.4.
- S. 152 ff: In Gleichung 4.43 ist im Argument der Spektralfunktion F nicht (k/ω), sondern (ω/k) richtig. Der Satz nach Abbildung 4.9 muss heißen: Ist k>1, so wird das Signal gestaucht, für k<1 wird es gestreckt. In der Abbildungsunterschrift zu Abbildung 4.10 b) ist k=2 richtig.
- S. 169:
Im Satz vor Gleichung 4.96 sollte es heißen:
Sind a und b Null,
so handelt es sich um lineare Transformationen.
Im Satz vor Gleichung 4.97 sollte es heißen: Die Transformation heißt unitär, wenn die Matrixelemente von T komplex sind und wenn gilt.
Im Satz vor Gleichung 4.98 sollte es heißen: Die Transformation heißt othogonal, wenn die Matrixelemente von T reell sind und wenn gilt. - S. 177:

- S. 178: Eine Matlab-Funktion zur Ermittlung einer orthogonalen Haarmatrix nach Gleichung 4.120 (programmiert von Enrico May). Es wird eine rekursive Bildungsvorschrift über das Kroneckerprodukt verwendet. Das Kroneckerprodukt (nach Leopold Kronecker) C = A ⊗ B ist definiert als C = (Au,v·B), das heißt, jedes Element Au,v der Matrix A wird mit der Matrix B multipliziert. Das Ergebnis ist wieder eine Matrix, allerdings größerer Dimension.
- S. 178: Eine Mathcad-Funktion zur Ermittlung einer orthogonalen Haarmatrix. Es wird wieder die rekursive Bildungsvorschrift über das Kroneckerprodukt verwendet.
- S. 186: Die Abbildung 4.33 ist korrigiert, im Text unter Abb. 4.33 ist 4× N durch n zu ersetzen.
- S. 194:
Die Gleichung 4.131 ist korrigiert:
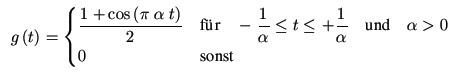
Gábor verwendete eine modifizierte Gaußglocke, Gleichung 4.132:
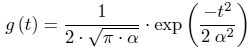
- S. 197: Auf Karten mit großen Maßstäben (zum Beispiel Maßstab 1:100 bzw. kleine Maßstabszahl 100) können Details gut erkannt werden, sie geben aber keinen Überblick über das Gebiet; Karten mit kleinen Maßstäben hingegen (zum Beispiel Maßstab 1:1.000.000 bzw. große Maßstabszahl 1.000.000) können keine Details enthalten, aber einen guten Überblick geben.
- S. 204: In der Gleichung 4.156 zur Berechnung von fn sind die oberen Summationsgrenzen zu ändern: j-Summe ld(N)-1 und k-Summe 2j-1.
- S. 205:

- S. 212 (Übung 46): Hier sollte die Formel 4.109 in leicht veränderter Form verwendet werden F = DCT·B·DCTT. Dann ist das Spektrum leichter interpretierbar. Für die Rücktransformation ist dann B´ = DCTT·F·DCT zu verwenden.
- S. 223: Der TPz Fuchs ist natürlich kein Kettenfahrzeug, sondern ein Radfahrzeug.
- S. 242 (Lösung zu Übung 11): Die Entropie bei zwei Würfeln beträgt 3,27 bit, bei drei Würfeln 3,6 bit. Bei drei Würfeln finden wir für die Standardabweichung 2,96.
- S. 243 (Lösung zu Übung 13): Als Verteilungsfunktion ergibt sich für x≥0 die Funktion F(x)=1-exp(-λx). Das 3. normierte Zentralmoment ist nicht abhängig von λ, sondern stets 2.
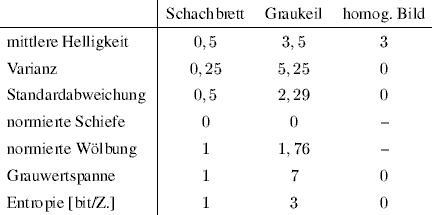
- S. 245 (Lösung zu Übung 17):
- S. 250 (Lösung zu Übung 32): Für die Fourierreihenkoeffizienten finden wir ak=4·sin(k2πd)/(kπ). Entsprechend ist dann im Summanden der Näherungsfunktion fapp(t) als Faktor vor dem Sinusterm 4/(kπ) zu schreiben.
- S. 256 (Lösung zu Übung 40):
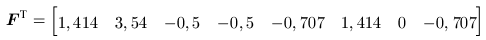
Prof. Dr. B. Meffert
Dr. O. Hochmuth
Rainer Schnabel
Anne Wegerich
Enrico May
Sascha Stübing
Вадим Баербах